论文Impossibility of Distributed Consensus with One Faulty Process证明了在异步系统中,哪怕只允许非拜占庭错误,只要有一个进程出错,那么系统就不一定能达成共识,也就是不满足 termination 要求。而在同步系统中,即使是拜占庭条件下却能够达成。
论文概要
定义一个异步系统
首先,FLP 定义了一个异步系统,它应该满足如下的特点:
- 非拜占庭的 Fail-stop 模型
- 最多一个进程失败
- 可靠通信、原子广播
即通信最终会被送达,且仅被送达和西欧s一次。但是消息可任意延迟、可乱序。例如基于 TCP 的通信并不满足这个条件,因为 TCP 承载的消息是不可以乱序的。 - 异步通信
没有时钟、不能时间同步、不能使用超时。
此外,进程之间还不能探测失败,因为无法判定一个异步进程到底是宕机了还是只是算得太慢。
系统中包含一系列进程,进程之间通过全局消息队列,称为 message buffer 进行通信。例如进程 p1 可以用 send(p2, m) 向进程 p2 发送消息 m,进程 p2 通过持续不断 receive(p2) 来获取自己的消息,并 event(p2, m) 来执行这个消息。以上的过程称为一个 step,一系列连续的 step 组成一个 run。
如果一个进程 p 在一个 run 中能运行无数个 step,那么它是非故障的。
定义一个 configuration 为当前所有进程和 message buffer 的状态,也就是整个系统的状态。那么一个 step 就会使得系统从一个 configuration 到达另一个 configuration。当然,在上面的例子中,如果 p2 由于分区等原因接受不到消息,这时候就表示为 m 为 NULL,即 event(p2, NULL)。
一个 initial configuration 指的是所有进程从某个初始状态启动,并且 message buffer 为空。
这里的 p 可以看做 deterministic 的 transition function。这意味着每个进程后续进入什么状态,完全取决于它从 message buffer 中取到什么消息。
假定所有进程试图达成一个 {0, 1} 的某个值上达成一个决议,并输出到寄存器 yp。yp 的值为 {b, 0, 1},其中 b 表示未产生表决结果的初始状态。一旦 yp 从 b 变为 0 或 1,这个值就不再可以被修改。这些进程可以从各自的寄存器 xp 中读取初始值,这些初始值是 {0, 1}。
C 上的一个 schedule 是有限或无限的 event 的序列 σ,这个序列可以被依次应用到 C 上。由它产生的一系列 step 称为 run。如果σ 是有限的,得到的新的 configuration 称为从 C 是 reachable 的。定义能从初始 configuration 到达的 configuration 是 accessible 的。
某个 configuration C 能 reachable (后面也会说“可达”)的所有 configuration 中的 decision value 的集合是 V。这里的 decision value 就是 0 或者 1。
定义 v 是 V 的势,可以说这个 configuration 是 v-valent 的。这里的 valent 在化学中被翻译为“价”,比如三价铁,四价铬。如果 V 中只有一个元素,那么就是 univalent。根据这个元素是什么,可以分为 0-valent 和 1-valent。如果 V 中有两个元素,就是 bivalent。
我们期望所有的正常进程最终都能达成正确的决议,但实际上 FLP 定理的证明中构造了一种情况,即使某些进程能够最终进入 univalent 的这一点都无法保证。
A configuration C has decision value v if some process p is in a decision state with y_p = v。
一个共识算法是部分正确的,当
- 所有 accessible 的 configuration 都有相同的 decision value。
- 所有 accessible 的 configuration 里面不能只有 0 或者 1,不然这样我搞一个系统永远输出 0,那不是永远部分正确了么?不考虑这样的平凡解。
定义一个共识算法是完全正确的,当它是部分正确的,此外还能满足终止条件。
整个的 FLP 定理的证明分为三个引理。
第二三引理类似于归纳法:
- 引理二先证明任意共识算法 P 都不能保证 initial configuration 都是 univalent。
- 然后引理三证明从 bivalent 能得到 bivalent。
这个归纳法我觉得很妙。另外,第三个引理的构造也很妙。
第一个引理
第一个引理很直观,从 C 开始有两个 schedule σ1 和 σ2,执行它们分别得到 C1 和 C2。我们再假定执行 σ1 和 σ2 的进程集合是不相交的,那么 σ2 又可以被应用到 C1 上,σ1 也可以被引用到 C2 上,这会导致得到相同的 configuation C3。
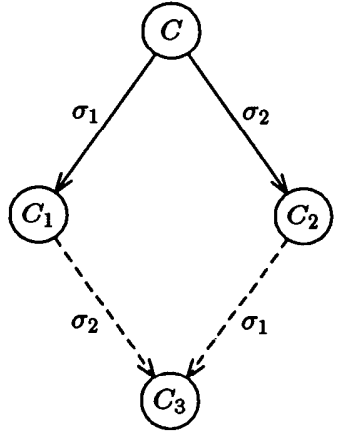
证明很简单,因为 σ1 和 σ2 彼此独立没有交集,这个对 Lamport 时钟有了解的都能够想明白。
第二个引理
首先,定义一个 run 是 admissible 的,如果最多一个进程故障了,并且所有其他非故障的进程都收到了所有的消息。
第二引理证明了在有一个进程失败的系统中,对于任意的共识算法 P,一定存在一个 bivalent initial configuration。这就是在说这样的系统中,同样的 initial configuration 可能运行出不同的结果。
证明用到了构建相邻环的思路,用大白话讲一下就是反证法假设系统从某个 univalent 开始,根据部分正确的条件2,要求有两个 configuration 为 C0 和 C1 分别是 0/1-valent 的。论文中指出,必然存在 decision value 为 0 的系统 C0 和为 1 的系统 C1 只差一个进程 p 。
例如三个进程的初始状态 xp = {1, 1, 0} 和 xp = {1, 0, 0} 就只差一个 p2。然后假设通过某个 Quorum 的共识算法,前者是 1-valent,后者是 0-valent。当然这里也可以用其他的算法让前者 0-valent,后者 1-valent,虽然这样很反直觉,但其目的主要是说明这样的 p2 是存在的。
现在假设 p2 故障了,也就是它不能运行哪怕一个 step,或者说不能 send 或者 receive 任何消息了。这样 C0 和 C1 在排除掉这个 p2 之后其实是一样的。
然后尝试以 C0 或 C1 为 initial configuration 来进行 admissible deciding run。那么 C0 和 C1 必然会进入同一个值,假如令它为 1,那么 C0 这个原本 0-valent 的 configuration 中的 decision value 就是 {0, 1} 了。这样 C0 就不是 univalent 的了,从而推出矛盾。
总而言之,第二个引理描述了对于任意的共识算法 P,一定存在 0-valent 的 configuration 和 1-valent 的 configuration 只差一个进程,令这个进程故障,那么就会得到一个 bivalent。所以对于 P,只要考虑一个故障节点,它就不能保证 initial configuration 都是 0-valent 和 1-valent 的。
第三个引理
第三个引理承接了第二个引理。它证明了从一个不确定的状态开始,也会得到不确定的状态。也就是说,在某种情况下,如果 C 是 bivalent 的,那么从它可达的所有 configuration 的集合 D 中包含一个 bivalent 的 configuration。
这个证明也分为两个小步骤。但整体上,依旧是使用反证法的:
- 证明
D中包含了 0-valent configuration 和 1-valent configuration。 - 证明
D中包含一个 bivalent 的 configuration。
首先定义事件 e=(p,m),它可以被 apply 到 C 上。那就可以分出:
- 集合1:不对
C应用e可达的 configuration 的集合E。 - 集合2:对
E中的 configuration 应用e可达的 configuration 的集合D。
【Q】这里,原文中使用花体字 D 和 E 来代表这里我说的 D 和 E。非花体字的 D 和 E 表示里面的一个 configuration,但实际上没有多大的作用,所以我就省略了。对于特定的元素 Di 或者 Ei,我还是使用了原文中的写法。
注意到,因为 e 能应用到 C,并且可以被任意延迟,所以它肯定也能应用到 E。
使用反证法,假设 D 中不含有 bivalent 的 configuration,也就是它里面的每个 configuration 都是 univalent 的。
现在假设,Ei 是从 Ci 可以 reachable 的某个 i-valent 的 configuration。由于 Ci 是 bivalent 的,所以 E0 和 E1 肯定是存在的。现在讨论 Ei:
- 如果
Ei属于E,那么对它应用e得到Fi,则根据 集合2 的特性,Fi肯定就属于D了。 - 如果
Ei不属于E,说明Ei已经在之前收到过消息e了。那么它会先到达一个同样属于D的 configurationFi,然后再到达Ei。
总而言之,无论走那条路,得到的 Fi 的 configuration 都是落在集合 D 中的。并且 Fi 是 i-valent 的,因为 Fi 属于 D,而根据假设,D 又不是 bivalent 的。
那既然开始的集合 C 是 bivalent 的,最后又都会落到同一个集合中,那么 D 中肯定既有 0-valent 又有 1-valent 的 configuration。这里为止和假设还是不矛盾的,因为我们需要证明 D 中包含一个 bivalent 的 configuration。注意这里的区别,valent 的概念是对 configuration 说的,而 D 是 configuration 的集合。
定义两个 configuration 相邻,如果第一个 configuration 可以通过一个 step 得到另一个。
简单的推导可知,E 中一定存在相邻的两个 C0 和 C1,对于这两个 Ci,D0=e(C0) 是 0-valent,D1=e(C1)是 1-valent 的。不失一般性地,设 C1=e'(C0),其中 e'=(p',m'),当然反过来假设也可以。回顾前文,这里的 p 表示进程 process。
我们可以得到一个如下图中实线所表示的有向图,但是否有虚线所示的关系是不确定的,所以要展开讨论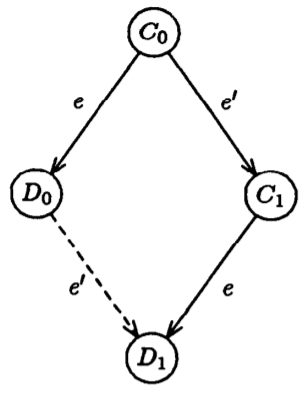
- 如果
p不等p',可以将它们划分到两个不相交集合中。所以根据引理1,可以得到D1=e'(D0)(上图中的虚线)。那么这也就意味着从一个 0-valent 的节点到达一个 1-valent 的节点,而这是不可能的,因为 0-valent 的后继只能是 0-valent 的。 - 如果
p等于p'了,考虑任意从 C0 开始的 finite deciding run,并且在这其中 p takes no steps。
我理解这里的 p takes no steps 就是假设 p 宕机了。但是从C0到D0和从C0到C1都要源于 p 去进行的 step。
假定这个 run 对应的 schedule 是σ。那么从C0就能通过σ到达一个Aconfiguration。
看图的左下部分,对于这个A状态应用e,可以到达E0。因为根据引理1,因为 p 和 D0 中的进程是不相交的,所以对D0应用σ得到E0。同理,可以构造右边的一个E1,从而发现A既可以变到E0又可以变到E1,A 是 bivalent 的。但是一开始我们说 A 是 deciding 的,所以它一定是 univalent 的。
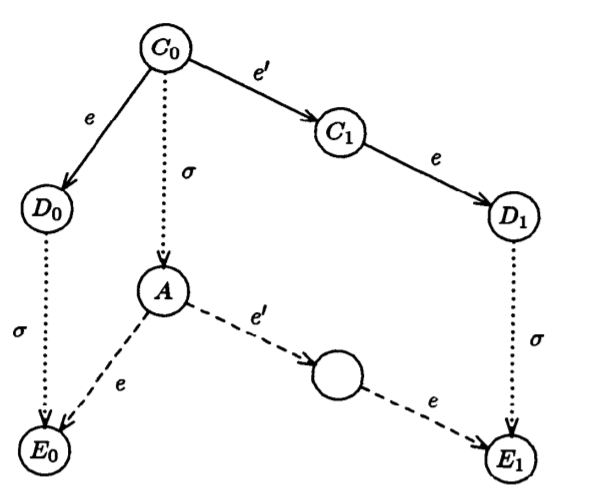
Any deciding run from a bivalent initial configuration goes to a univalent configuration, so there must be some single step that goes from a bivalent to a univalent configuration. Such a step determines the eventual decision value. We now show that it is always possible to run the system in a way that avoids such steps, leading to an admissible nondeciding run.

FLP 定理的现实意义
FLP 定理使用的异步模型是很严格的。它假设了确定性的算法中不能使用任何时钟或者超时来判断可能的崩溃节点。实际上引入这些方法进行检测,哪怕检测结果可能有时是错误的,那么共识问题就是有解的。

